Can the Ka of a Natural Indicator Be Determined by Spectrophotometer

American Periodical of Analytical Chemistry
Vol.05 No.17(2014), Article ID:52618,xi pages
10.4236/ajac.2014.517135

Spectrophotometric Conclusion of the pKa, Isosbestic Point and Equation of Absorbance vs. pH for a Universal pH Indicator

L. E. Vidal Salgado, C. Vargas-Hernández

Laboratory of Optical Backdrop of Materials (POM), National University of Colombia, Manizales, Colombia

Electronic mail: cvargash@unal.edu.co

Copyright © 2014 by authors and Scientific Inquiry Publishing Inc.

This piece of work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 3 Oct 2014; revised xx Nov 2014; accepted seven December 2014

Abstruse

The pKa and the isosbestic point of the universal pH indicator Carlo Ebra 1-xi (catalog number 45712) were determined using UV-Vis spectrophotometry. Aqueous buffer solutions with pHs ranging from 3.83 to 10.85 were mixed. Four methods―2 graphical and two mathematical― were used to gauge the acid dissociation abiding (pKa) and isosbestic point using absorbance measurements. The equation for the dependence of the absorbance on pH at l = 600 nm was obtained using calibration curves. The resulting average pKa of the iv methods was eight.277 with a standard deviation of 0.1728. The results obtained using the mathematical methods were very similar, with a deviation of 0.0014; the boilerplate pKa adamant using these methods was 8.263 ± 0.001. The literature contains no previous reports of the pKa of this indicator. The isosbestic point occurs at a wavelength of 494 nm, with an absorbance of 0.46.

Keywords:

Pattern of Buffers, Spectrophotometric Titration, Conclusion of pKa, Isosbestic Point, Universal pH Indicator

1. Introduction

The value of the acid dissociation constant (pKa) is an important parameter that indicates the caste of ionization of molecules in solution at different pH values. Many chemical, physical and biological backdrop of natural and synthetic compounds are governed by the interactions of acidic and basic groups. In such compounds, the pKa controls many aspects of metabolism and even transport beyond membranes; therefore, its study is of significant interest in biology, pharmaceutics, medicine, and numerous other scientific fields. Zscherp et al. [i] determinedthe transient pKa changes of a single amino acid side chain in bacteriorhodopsin, a protein important in photosynthesis. Baran et al. [2] investigated the pKa of amino acid complexes and their human relationship to atomic orbitals. Several groups [3] - [half-dozen] have investigated the behaviors of different drugs, including those used against cancer, and the dependence of their behaviors on their pKa values. Novel pKa determination methods that apply pH colorimetric indicators have too been reported [7] - [9] .

Two main methods exist for determining the pKa of a compound: potentiometric titration and spectrophotometric titration. The main advantage of the second method is the power to obtain a titration curve, which allows for estimation at any point without necessitating an experiment. In contrast, potentiometric titration requires knowledge of the equilibrium concentrations of the reagents, which are not necessary in spectrophotometric titration because the ratio of the concentrations of the basic and acidic parts is obtained from the results of absorbance measurements. When the mixing of a solution and an indicator is investigated spectrophotometrically, the mixture absorbs in the UV region (250 - 380 nm), whereas the indicator, depending on the pH of the solution, absorbs in the visible region (380 - 700 nm). The pKa can be determined from the spectrophotometric data using unlike methods. Meloun et al. [10] [11] depict multiwavelength analysis and nonlinear least squares regression methods. Computational methods, such as SQUAD (84) 16 and SPECFIT/32, and some new methods [12] - [fifteen] have also been developed.

Theoretical Foundations

When an acrid HA is dissolved in water, equilibrium is established:

(1)

The acid HA transfers a proton to h2o, and it becomes the anion A⁻. This anion tends to retrieve the proton and acquit every bit a base of operations; A⁻ is therefore referred to equally the "cohabit base" of acrid HA, and HA and A⁻ are referred to as a "conjugate pair" [16] [17] . A shift of the equilibrium in Equation (1) to the right or left depends on the relative strengths of the HA and H₃O⁺ acids. The "force" of an acid refers its tendency to transfer protons, and one method of standardizing its force is to compare the protonation country when it interacts with water. The outcome of this comparison is expressed equally the "acid dissociation abiding," Ka, equally follows:

(ii)

Ka is a constant of the stoichiometric equilibrium defined in terms of the concentration ratio [A⁻]/[HA], which can be determined spectrophotometrically [eighteen] . If a solution with a total concentration of indicator C_T becomes very acidic, all indicator exists equally HA. The absorbance of the solution at a given wavelength fifty is given by

(three)

where e_HA is the molar absorptivity of HA at wavelength l and b is the width of the cell containing the solution. If the solution is besides basic, the same concentration of indicator is converted entirely into A⁻ and the absorbance at the same wavelength is given past

(4)

where is the molar absorptivity of A⁻. At an intermediate pH, the absorbance is given past

(v)

where the total concentration is defined in any condition every bit

(half dozen)

For a given C_T, Equations (3)-(6) tin exist combined to obtain

(vii)

This relationship must be evaluated at multiple wavelengths, including one where HA absorbs appreciably but A⁻ does not, one where A⁻ is much more than absorbent than HA, and another where the absorbance of the two species is approximately the same. The pH (−log[H₃O⁺]) of the solutions must be in the transition range of the indicator and then that both HA and A^-are present in appreciable concentrations. Ka tin be evaluated graphically by converting Equation (2) to logarithmic grade:

(viii)

In addition, the combination of Equation (7) and the definition of pKa = −log Ka results in

(9)

Therefore, a graph of vs. pH has an ideal slope of one. If this condition holds, the y-axis intercept gives the negative pKa directly. All the same, the experimental slope is not usually exactly i, necessitating that the pH values of the measurements be extrapolated to pH = 0 (which is typically a factor of 10⁶ in concentration), resulting in a very large fault for the pKa value. In contrast, if the to the lowest degree-squares equation is solved for the intercept with the ten-axis, where, the pKa results are obtained with very little uncertainty. At this intercept, [A⁻]/[HA] = 1, indicating that the concentrations of the acrid and its conjugate base are equal. When HA is a strong acrid, a value for Ka in aqueous solutions cannot be divers, because HA molecules cannot be detected; the value of Ka is therefore very high or infinite. In contrast, a very depression value indicates that the dissociation Ka involves a very small fraction of the total acrid nowadays. The isosbestic point is the signal on the graph of absorbance vs. pH where the molar absorption coefficients of the species in equilibrium are the same.

2. Experimental Methods

Grooming of solutions. 3 families of buffers covering the pH range between 2.3 and 10.85 were prepared using four solutions of citrate buffer at pH 2.3, 3.05, 4.37 and 5.4 containing citric acrid and its conjugate base. Table 1 shows the reactants and the proportions used to prepare the citrate buffer.

The calculation model is based on the Henderson-Hasselbach Equation (x) and on the final concentration Cf of the acrid and its conjugate base (Equation (4)):

(ten)

(11)

To calculate the mass of the reagents, Equations (10) and (11) are solved simultaneously by setting the desired pH and concentration (Cf). These equations were solved using a program developed in LabVIEW for greater agility. The results for the formulations are shown in Table ii.

The calculated pH values exhibited some differences, specially at college pH levels, as illustrated in Figure ane. The standard deviation of the data was 0.728 pH units.

A 2nd phosphate buffer was prepared using ii stock solutions: 100 ml of 0.two 1000 monosodium phosphate and disodium phosphate (Table 3), which were mixed to obtain buffer solutions with pH six.5, 7.08 and 7.7.

The grooming of stock solutions required two.84 one thousand of monosodium phosphate (monohydrate) and 2.76 g of disodium phosphate, which were so diluted with distilled-and-deionized h2o to a volume of 100 ml. Finally, these stock solutions were combined in the proportions listed in Table 4.

Table 1. Reagents used in the training of the citrate buffer.

Table 2. Preparation of the citrate buffer at unlike pH levels and concentrations.

Table 3. Reagents used to prepare the phosphate buffers.

Table iv. Preparation of phosphate buffer at unlike concentrations and pH.

Figure ane. Comparison between the calculated and obtained pH values for citrate buffers.

Figure 2 shows the curves of the calculated and obtained pH values for the prepared phosphate buffers. The obtained pH values were higher than expected, with a standard deviation of 0.434 pH units.

The third prepare of solutions consisted of ammonium buffers composed of a mixture of ii stock solutions: ammonia and ammonium chloride. The calculations were like to those used for the preparation of the phosphate buffers. Tabular array five shows the details of the training.

Figure 3 shows the curves for the calculated and experimental pH values for the ammonium buffer solutions. The obtained values were higher than expected, with a standard deviation of 0.624 pH units.

Even though the buffers did not accept pH values equal to the calculated values, they were very stable and retained their constant pH value for months. The well-nigh important factor for the spectrophotometric decision of pKa is that the pH be known and stable.

3. Results and Discussion

Spectrophotometric measurements. Absorbance measurements were performed using a Thermo Scientific Evolution 300 UV-Vis spectrophotometer in the wavelength range between 380 and 700 nm (visible spectrum). In this study, universal indicator pH one - 11 (catalog number 45712, Carlo Ebra, Milano, Italian republic) was used. The pH measurements were performed using an Oakton pH 2700 pH meter. Plots of absorbance against l for the universal indicator in buffers with different pH levels are illustrated in Figure iv.

Neither the chemical composition of this indicator nor its dissociation constant was provided by the manufacturer. Therefore, spectrophotometric measurements were performed to determine its pKa, and 2 graphical and two analytical methods were applied. The results obtained using the unlike methods were compared, and the

Figure 2. Comparison of the calculated and measured pH values for the phosphate buffers.

Table 5. Preparation of ammonium buffer at different concentrations and pH.

Effigy three. Comparing of the measured and calculated pH values for ammonium buffers.

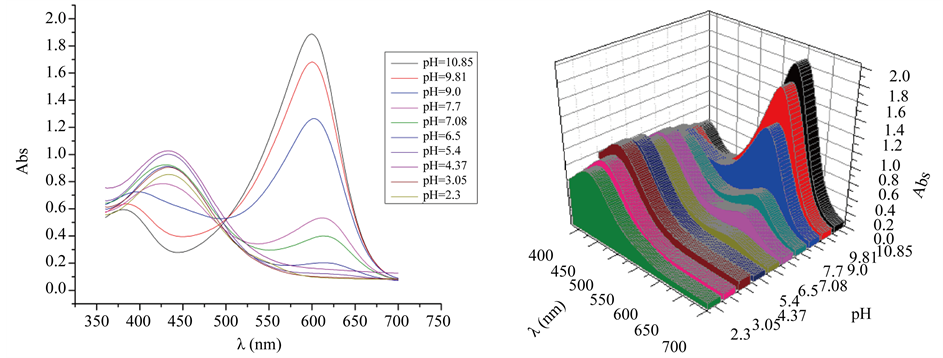
Figure iv. Absorbance spectra of the universal indicator pH 1 - 11 at different pH levels.

nearly suitable pKa value was adamant. The first method was to accept the spectra of the species with farthermost pHlevels (pH = 2.3 and pH = x.85 in this case) and determine the wavelengths of maximum absorbance, every bit illustrated in Effigy 5.

As illustrated in Figure 5, the absorbance spectrum of the solution of pH = 2.3 exhibited a elevation at 434 nm; the peak of the basic solution occurred at 600 nm. The plot of the absorbance vs. pH at these wavelengths is presented in Figure 6.

The pKa was obtained by determining the pH of the signal of intersection of the ii linear curves equally shown in Figure six. To decide this point, the linear equations of the ii points closest to the crossing at each bend were solved:

(12)

where

(13)

Thus,

pKa = viii.0792

The second method was to plot vs. pH (Equation (9)), where A_HA is the ab-

Figure 5. Absorbance spectra of universal indicator solutions at extreme pH levels.

Effigy 6. Plot of absorbance vs. pHat wavelengths of 434 and 600 nm.

sorbance of the acid solution, A_i is each of the intermediate absorbances and A_A is the absorbance of the bones solution. For the best results, the wavelength where the difference between the absorbance curves of the acidic and bones solutions is greatest must exist chosen, which, in this example, corresponds to fifty = 600 nm.

When linear regression of the data is performed, the resulting equation is

(fourteen)

A graph of the information and the linear regression are shown in Effigy 7.

The pKa is obtained from the intercept of the line with the x-axis according to the equation

(15)

In add-on,

We have

Figure 7. Linear regression of log[(A_HA − A_i)/(A_i − A_A)] vs. pH.

(xvi)

resulting in

The third method is to use Equation (8) solved for pKa:

(17)

where pH_i is the intermediate value between the acid and alkaline metal farthermost values. The intermediate pH selected was pH = 7.seven, which was called because of the substantial coincidence of its isosbestic point with those of the farthermost-pH solutions, equally illustrated in Figure 8.

Equation (16) was then practical to all wavelengths, resulting in the graph shown in Figure 9.

The average of all of the information gives pKa = eight.26272. The isosbestic signal was determined by taking the wavelength value where the standard deviation of absorbance was minimal. The isosbestic point appeared at a wavelength of 494 nm.

The 4th method, which is similar to the tertiary, was based on the absorbance of 3 solutions with dissimilar pH values (i.east., a very acidic, a very bones and one intermediate-pH solution) at the same wavelength. The pKa was obtained by substituting these values into the following equation:

(18)

where I represents the lowest pH value (in this example, 2.three); a corresponds to the difference between the intermediate pH and the I value (a = 7.vii − 2.3 = five.4); b is the difference between the almost alkaline pH and the most acidic (b = 10.85 − 2.3 = eight.55); A₁, A₂ and A_three are the absorbances at each pH value for a given wavelength. The calculated pKa data are plotted as a office of wavelength in Figure 10.

The average of all of the data gave pKa = eight.26466, which is very similar to that adamant using the third method. Table half-dozen shows a summary of the results obtained using the four methods.

The boilerplate value obtained using the iv methods correspond to a pKa of eight.277. The results obtained using these equations were like, with a standard deviation of only 0.00137; thus, the average of these two values was taken equally the virtually appropriate result for the pKa of the indicator in this report:

Finally, an equation for the relationship between the absorbance and the pH at a wavelength of 600 nm was obtained. This wavelength was selected because information technology is the value where the absorbance is highest and produces the greatest rate of change in Equations (17) and (18). The absorbance every bit a function of pH was obtained via not-

Figure eight. Absorbance curves for the acidic, basic, and intermediate pH solutions.

Figure nine. Curve of values obtained from Equation (17).

Effigy 10. Graph of pKa vs. 50 for pKa values calculated using Equation (18).

linear curve fitting in OriginProusing the Gaussian equation, which provided the best fit to the data. Effigy 11 shows the data and the curve of best fit.

The data from the best-fit equation are shown in Tabular array 7.

Therefore, the equation tin can be written as

Table 6. Comparison of the pKa information obtained using the dissimilar methods.

Table 7. Equation modeling of absorbance as a function of pH.

Figure 11. Equation for the absorbance vs. pH at λ = 600 nm.

(19)

iv. Conclusion

The awarding of spectrophotometric titration allowed the acid dissociation abiding of universal pH indicator 1 - eleven from Carlo Ebra to be determined. Iv methods of assay―two graphical and two mathematical methods―were used and produced results with adept similarity, especially in the cases of the two mathematical methods. Some colorimetric pH indicators, such every bit bromothymol blueish in acidic solutions, are unstable over long periods of time, whereas the studied universal indicator retains its color even months after being exposed to highly acidic solutions. This property and the meaning color variation make the evolution of a technique for spectrophotometric measurement of pH interesting. An equation was obtained for the human relationship between absorbance and pH with a very low dispersion, and the isosbestic point was determined.

References

1. Zscherp, C., Schlesinger, R., Tittor, J., Oesterhelt, D. and Heberle, J. (1999) In Situ Determination of Transient pka Changes of Internal Aminoacids of Bacteriorhodopsin by Using Time-Resolved Attenuated Total Reflection Fourier- Transform Infrared Spectroscopy. Biophysics: Proceedings of the National Academy of Sciences, 96, 5498-5503.
2. Baran, Y., Baran, S. and Kemal, N. (1997) Spectofotometric Determination of the pKa Values of Some Aminoacid Complexes of Pentacyanoferrate (II) and Pentacyanoruthenate (2). Journal of Chemical science, 21, 105-110.
3. Meloun, G., Bordovská, S. and Vrana, A. (2007) The Thermodynamic Dissociation Constants of the Anticancer Drugs Camptothecine, 7-Ethyl-ten-hydroxycamptothecine, 10-Hydroxycamptothecine and 7-Ethylcamptothecine by the Least- Squares Nonlinear Regression of Multiwavelength Spectrophotometric pH-Titration Data. Analytica Chimica Acta, 584, 419-432. http://dx.doi.org/x.1016/j.aca.2006.11.049
4. Meloun, M., Bordovská, South. and Galla, L. (2007) The Thermodynamic Dissociation Constants of Four Non-Steroida- lanti-Inflammatory Drugs by the Least-Squares Nonlinear Regression of Multiwavelength Spectrophotometric pH-Ti- tration Data. Periodical of Pharmaceutical and Biomedical Assay, 45, 552-564. http://dx.doi.org/ten.1016/j.jpba.2007.07.029
5. Mitchell, R.C., Salter, C.J. and Tam, K.Y. (1999) Multiwavelength Spectrophotometric Decision of Acid Dis- sociation Constants Part III: Resolution of Multi-Protic Ionization Systems. Journal of Pharmaceutical and Biomedical Assay, 20, 289-295. http://dx.doi.org/x.1016/S0731-7085(99)00041-two
6. Tam, K.Y., Hadley, One thousand. and Patterson. W. (1999) Multiwavelength Spectrophotometric Determination of Acid Dissocia- tion Constants Part IV: Water-Insoluble Pyridine Derivatives. Talanta, 49, 539-546. http://dx.doi.org/10.1016/S0039-9140(99)00010-vii
7. Amador-Hernández, J., Rojas-Hernández, A. Madaí, Eastward., De La Garza-Rodríguez, M., Velázquez-Manzanares, One thousand. and Medina-Vallejo, L.F. (2014) New Chemometric Strategies in the Spectrophotometric Conclusion of pKa. European Journal of Chemistry, 5, 1-5. http://dx.doi.org/ten.5155/eurjchem.5.1.1-5.901
8. Ivanov, V.M., Adamova, E.G. and Figurovskaya, V.Northward. (2010) Acid-Base of operations, Spectrophotometric, and Colorimetric Properties of 1, two-Dihydroxyantraquinonone3-sulfoacid (Alizarin Red S). Journal of Analytical Chemistry, 65, 473-481. http://dx.doi.org/10.1134/S1061934810050072
9. Kong, X., Zhou, T., Liu, Z. and Hider, R.C. (2007) pH Indicator Titration: A Novel Fast pKa Determination Method. Journal of Pharmaceutical Sciences, 96, 2777-2783. http://dx.doi.org/10.1002/jps.20959
10. Meloun, G., Bordovská, S., Syrový, T. and Vrána, A. (2006) Tutorial on a Chemical Model Building past To the lowest degree-Squares Non-Linear Regression of multiwavelength Spectrophotometric pH-Titration Information. Analytica Chimica Acta, 580, 107- 121. http://dx.doi.org/x.1016/j.aca.2006.07.043
11. Meloun, Thousand., Bordovská, S. and Syrovy, T. (2007) A Novel Computational Strategy for the pKa Estimation of Drugs by Non-Linear Regression of Multiwavelength Spectrophotometric pH-Titration Data Exhibiting Small Spectral Changes. Journal of Physical Organic Chemistry, 20, 690-701. http://dx.doi.org/10.1002/poc.1235
12. Meloun, M., Ferencíková, Z. and Vrána, A. (2011) Determination of the Thermodynamic Dissociation Constant of Capecitabine Using Spectrophotometric and Potentiometric Titration Information. Periodical of Chemical Thermodynamics, 43, 930-937. http://dx.doi.org/10.1016/j.jct.2011.01.012
13. Panigrahi, S., Suna, P. and Misra, P.Thousand. (2012) Effect of Organized Assemblies, Part Viii: Spectrophotometetric Written report on the Effect of Micellar Media on the pK of Some Substituted N-Benzylideneanilines. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 415, 349-357. http://dx.doi.org/10.1016/j.colsurfa.2012.08.051
14. Zapata, 50., Kalembkiewicz, J. and Sitarz-Palczak, East. (2009) Studies on Equilibrium of Anthranilic Acid in Aqueous Solutions and in Ii-Phase Systems: Aromatic Solvent-Water. Biophysical Chemistry, 140, 91-98. http://dx.doi.org/x.1016/j.bpc.2008.11.012
15. Smith, S.A. and Pretorius, W.A. (1994) Spectrophotometric Determination of pKa Values for Fluorescein Using Activity Coefficient Corrections. H2o SA, 28, 395-402.
16. Skoog, D. and Leary, J. (1994) Análisis Instrumental. McGraw-Colina, Madrid.
17. Harris, D.C. (1999) Quantitative Chemical Analysis. West.H. Freeman, New York.
18. Vogel, A. (1969) Química Analítica Cuantitativa: Teoría y Práctica. Editorial Kapelusz, Buenos Aires.

ortonmagnstowiter.blogspot.com

Source: https://www.scirp.org/html/13-2201097_52618.htm

Share this post